4.1 Definición de series
4.1.1 Finita
En matemática, un conjunto finito es un conjunto que tiene un número finito de elementos. Por ejemplo {2, 4, 6, 8, 10} es un conjunto finito con cinco elementos. La cardinalidad o número de elementos de un conjunto finito es igual a un número natural.
Si un conjunto no es finito, entonces es infinito. Por ejemplo, el conjunto N = {1, 2, 3, ...} de los números naturales es infinito. Todo conjunto finito es un conjunto numerable, puesto que sus elementos pueden contarse, pero la recíproca es falsa: existen conjuntos infinitos y numerables (como el propio N).
Los conjuntos finitos son particularmente importantes en combinatoria.
Un conjunto finito A es aquel que puede ponerse en correspondencia biunívoca con el conjunto {1, 2, ..., n} para algún número natural n.
Que pueda establecerse una correspondencia biunívoca significa que los elementos de A y los de {1, 2, ..., n} pueden emparejarse uno a uno, sin que sobre ningún elemento de ninguno de los dos conjuntos. Al número n se le denomina el cardinal de A (o su cardinalidad, su potencia, etc.), y se denota por card(A), |A| o #A. El conjunto vacío ∅ no tiene elementos, |∅| = 0, por lo que también es finito.
La definición de conjunto finito en teoría axiomática de conjuntos presenta algunas sutilezas (véase Conjunto infinito).
4.1.2 Infinita
El concepto de infinito aparece en varias ramas de la filosofía,1 la matemática y la astronomía,2 en referencia a una cantidad sin límite o final, contrapuesto al concepto de finitud.3
En matématicas el infinito aparece de diversas formas: en geometría, el punto al infinito en geometría proyectiva y el punto de fuga en geometría descriptiva; en análisis matemático, los límites infinitos, olímites al infinito; y en teoría de conjuntos como números transfinitos.
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza; dada una parte propia de los mismos, ésta contiene un número de elementos menor que todo el conjunto. Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto. Sin embargo, esa propiedad "intuitiva" de los conjuntos finitos no la tienen los conjuntos infinitos, y formalmente decimos que:
- Un conjunto
 es infinito si existe un subconjunto propio
es infinito si existe un subconjunto propio 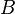 de
de  , es decir, un subconjunto
, es decir, un subconjunto 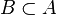 tal que
tal que 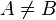 , tal que existe una biyección
, tal que existe una biyección  entre
entre  y
y 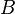 .
.
