areas
área es una medida de la extensión de una superficie, expresada en unidades de medida denominadas superficiales. Para superficies planas el concepto es más intuitivo. Cualquier superficie plana de lados rectos puede triangularse y se puede calcular su área como suma de las áreas de dichos triángulos. Ocasionalmente se usa el término "área" como sinónimo de superficie, cuando no existe confusión entre el concepto geométrico en sí mismo (superficie) y la magnitud métrica asociada al concepto geométrico (área).
Sin embargo, para calcular el área de superficies curvas se requiere introducir métodos de geometría diferencial.
3.1 áreas bajo la gráfica de una función
Definición de integral definida. Área bajo la gráfica de una función
Sea una función continua en el intervalo , tal que toma solo valores NO negativos en dicho intervalo ( ).
Nos planteamos el siguiente problema: ¿Como podemos calcular el area comprendida entre las rectas verticales de ecuaciones y , la grafica de la función y el eje X? El área que queremos calcular corresponde a la superficie coloreada de azul en la figura de abajo:
Este area es el valor de la integral entre y de y la denotamos por:
Esta integral se trata de una integral definida. Una integral definida es, por tanto, un número, mientras que una integral indefinida es una familia de funciones ( el conjunto de primitivas de la función que se integra ).
Veamos una manera de dar una solución aproximada al problema que nos planteabamos ( el calculo de dicha area ).
Dividimos el intervalo en intervalos de la misma longitud . Los limites de estos intervalos mas pequeños son:
donde .
Para contruyamos el rectangulo cuya base es el intervalo y cuya altura es de longitud .
Haciendo esto para , terminamos con rectangulos. La suma de sus areas es una aproximación al area bajo la grafica de que queremos calcular.
En general, cuanto mayor sea mejor aproximación sera la suma de las areas de los rectangulos a .
Así, cuando :
uno podria esperar que la aproximación obtenida sea peor que si se considera un número mayor de rectangulos, por ejemplo :
Llamemos a la suma de los rectangulos así construidos. Se tiene que:
Es decir, tiende a cuando el número de rectangulos, , tiende a infinito.
En todo lo que hemos visto hasta ahora hemos supuesto que la función toma valores NO negativos en el intervalo . ¿Que pasaría si tomase valores NO positivos en dicho intervalo? En este caso, ¿como podemos calcular el area comprendida entre las rectas verticales de ecuaciones y , la grafica de la función y el eje X?
Casi todo lo dicho con anterioridad para el caso seria aplicable al caso , pero ahora:
y el area sobre la grafica de la función es
siendo la integral definida NO positiva porque .
3.2 longitud de curva
Longitud de curvas planas
La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.
Definición:
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.
Cuando la curva es suave, la longitud de cada pequeño segmentos de recta se puede calcular mediante el teorema de Pitágoras y (dL)2=(dx)2+(dy)2, de tal forma que sumando todos los diferenciales resulta:
Definición:
Si f es suave en [a,b], la longitud de la curva de f(x) desde a hasta b es:
3.3 calculo de volúmenes de sólidos en revolucion
3.4 calculo de centroides
CENTROIDES El centroide es un punto que define el centro geométrico de un objeto. Su localización puede determinarse a partir de formulas semejantes a las utilizadas para determinar el centro de gravedad o el centro de masa del cuerpo, el centroide nos ayuda a encontrar el punto en el que se concentra las fuerzas que actúan sobre una figura irregular, o figuras geométricas no muy conocidas, por ejemplo el centroide nos ayudaría a encontrar el punto en el que se concentran las fuerzas de un puente
Se consideran tres casos específicos:
VOLUMEN. Si un objeto se subdivide en elementos de volumen dv, la localización del centroide para el volumen del objeto se puede determinar calculando los momentos de los elementos en torno a los ejes de coordenadas. Las formulas que resultan son:
X = “ x dv Y = “ y dv Z = “ z dv
“ dv “ dv “ dv
AREA. De manera semejante, el centroide para el area superficial de un boleto, como una planca o un casco puede encontrase subdividiendo el area en elementos diferentes dA y calculando los momentos de estos elementos de area en torno a los ejes de coordenadas a saber.
X = “ x dA Y = “ y dA Z = “ z dA
“ dvA “ dA “ dA
LINEA. Si la geomentria del objeto tal como una barra delgada un alambre, toma la forma de una linea, la manera de encontrar su centoide es el siguiente:
X = “ x dL Y = “ y dL Z = “ z dL
“ dL “ dL “ dL
viernes, 1 de julio de 2011
jueves, 9 de junio de 2011
4.1 Series
4.1 Definición de series
4.1.1 Finita
En matemática, un conjunto finito es un conjunto que tiene un número finito de elementos. Por ejemplo {2, 4, 6, 8, 10} es un conjunto finito con cinco elementos. La cardinalidad o número de elementos de un conjunto finito es igual a un número natural.
Si un conjunto no es finito, entonces es infinito. Por ejemplo, el conjunto N = {1, 2, 3, ...} de los números naturales es infinito. Todo conjunto finito es un conjunto numerable, puesto que sus elementos pueden contarse, pero la recíproca es falsa: existen conjuntos infinitos y numerables (como el propio N).
Los conjuntos finitos son particularmente importantes en combinatoria.
Un conjunto finito A es aquel que puede ponerse en correspondencia biunívoca con el conjunto {1, 2, ..., n} para algún número natural n.
Que pueda establecerse una correspondencia biunívoca significa que los elementos de A y los de {1, 2, ..., n} pueden emparejarse uno a uno, sin que sobre ningún elemento de ninguno de los dos conjuntos. Al número n se le denomina el cardinal de A (o su cardinalidad, su potencia, etc.), y se denota por card(A), |A| o #A. El conjunto vacío ∅ no tiene elementos, |∅| = 0, por lo que también es finito.
La definición de conjunto finito en teoría axiomática de conjuntos presenta algunas sutilezas (véase Conjunto infinito).
4.1.2 Infinita
El concepto de infinito aparece en varias ramas de la filosofía,1 la matemática y la astronomía,2 en referencia a una cantidad sin límite o final, contrapuesto al concepto de finitud.3
En matématicas el infinito aparece de diversas formas: en geometría, el punto al infinito en geometría proyectiva y el punto de fuga en geometría descriptiva; en análisis matemático, los límites infinitos, olímites al infinito; y en teoría de conjuntos como números transfinitos.
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza; dada una parte propia de los mismos, ésta contiene un número de elementos menor que todo el conjunto. Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto. Sin embargo, esa propiedad "intuitiva" de los conjuntos finitos no la tienen los conjuntos infinitos, y formalmente decimos que:
- Un conjunto
 es infinito si existe un subconjunto propio
es infinito si existe un subconjunto propio 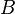 de
de  , es decir, un subconjunto
, es decir, un subconjunto 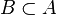 tal que
tal que 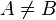 , tal que existe una biyección
, tal que existe una biyección  entre
entre  y
y 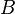 .
.
viernes, 3 de junio de 2011
4.2 Serie numérica y convergencia Prueba de la razón
SERIES NUM´ERICAS.
1. Convergencia.
Si {an} es una sucesi´on de n´umeros reales, se define la serie de t´ermino general an y
se escribe
P∞
n=1
an como:
∞X
n=1
an = lim (a1 + · · · + an).
Si este l´ımite de la n-´esima suma parcial a1 + · · · + an es finito, se dice que la serie es
convergente; si es infinito o no existe, que es divergente.
2. Convergencia absoluta.
Se dice que la serie
P
an es absolutamente convergente si la serie
P
|an| es convergente.
Toda serie absolutamente convergente es convergente.
Si una serie es absolutamente convergente, entonces cualquier reordenaci´on suya tambi´en lo es y tiene el mismo valor.
Se dice que una serie es condicionalmente convergente si es convergente, pero no
absolutamente convergente.
3. Propiedades.
• El car´acter (convergente o divergente) de una serie no cambia si se modifica un
n´umero finito de sus t´erminos.
• Para que la serie
P
an converja es necesario que lim an = 0.
• Si las series
P
an y
P
bn convergen, entonces:
P
an + bn y
P
λan, con λ ∈ R,
tambi´en, teni´endose:
X
(an + bn) =
X
an +
X
bn y
X
λan = λ
X
an.
4. Series geom´etricas y arm´onicas.
• Las series geom´etricas
P
r
n
convergen si |r| < 1 y divergen en caso contrario.
• Las series arm´onicas
P 1
nα
convergen si α > 1 y divergen en caso contrario.
5. Criterios de convergencia para series de t´erminos positivos.
• de comparaci´on:
Si a partir de un cierto lugar an ≤ k bn (resp. an ≥ k bn) y
P
bn converge (resp.
diverge), entonces
P
an tambi´en.
Si lim
an
bn
∈ R \ {0}, entonces
P
an y
P
bn tienen el mismo car´acter.
• del cociente:
Si lim
an+1
an
< 1 (resp. > 1), entonces
P
an converge (resp. diverge).
Typeset by AMS-TEX
12
• de Raabe (cuando lim
an+1
an
= 1):
Si lim n
1 −
an+1
an
> 1 (resp. < 1), entonces
P
an converge (resp. diverge).
• de la ra´ız:
Si lim n
√
an
< 1 (resp. > 1), entonces
P
an converge (resp. diverge).
• de condensaci´on:
Si {an} es decreciente, entonces
P
an y
P
2
n
a2n tienen el mismo car´acter.
6. Series alternadas.
Son las de la forma
P
(−1)
n
an o
P
(−1)
n+1
an, donde an > 0 ∀n ∈ N.
Criterio de Leibnitz: ”Si {an} es una sucesi´on decreciente y tiende a 0, entonces la
serie alternada converge”.
Adem´as, si s es el valor de una serie alternada y sn su n-´esima suma parcial, entonces:
|s − sn| ≤ an+1.
Publicado por sinuhe en 17:28
4.3.- serie de potencias
Definición
Una serie de potencias alrededor de x=0 es una serie de la forma:
http://upload.wikimedia.org/math/3/5/4/3544568cd59d64eb4cf3a9db6a049a5a.png
Una serie de potencias alrededor de x=c es una serie de la forma:
http://upload.wikimedia.org/math/9/5/4/95423a77cd9eefe02337c916df37dde2.png
En el cual el centro es c, y los coeficientes an son los términos de una sucesion.
Ejemplos:
La serie geométrica:
http://upload.wikimedia.org/math/d/4/f/d4f70d3ca5016b9df8ec18268fc2a4b7.png
es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
La serie de potencias:
http://upload.wikimedia.org/math/1/5/3/15347bc9ef25f8874a0a52ca60a81271.pnges
absolutamente convergente para todo
La serie de potencias:
http://upload.wikimedia.org/math/6/9/9/699cdfcbdf8d1aa19e3ae485987319ef.png
solamente converge para x = 0
Una serie de potencias alrededor de x=0 es una serie de la forma:
http://upload.wikimedia.org/math/3/5/4/3544568cd59d64eb4cf3a9db6a049a5a.png
Una serie de potencias alrededor de x=c es una serie de la forma:
http://upload.wikimedia.org/math/9/5/4/95423a77cd9eefe02337c916df37dde2.png
En el cual el centro es c, y los coeficientes an son los términos de una sucesion.
Ejemplos:
La serie geométrica:
http://upload.wikimedia.org/math/d/4/f/d4f70d3ca5016b9df8ec18268fc2a4b7.png
es una serie de potencias absolutamente convergente si | x | < 1 y divergente si | x | > 1 ó | x | = 1
La serie de potencias:
http://upload.wikimedia.org/math/1/5/3/15347bc9ef25f8874a0a52ca60a81271.pnges
absolutamente convergente para todo
La serie de potencias:
http://upload.wikimedia.org/math/6/9/9/699cdfcbdf8d1aa19e3ae485987319ef.png
solamente converge para x = 0
Publicado por sanchez franco daniel en 10:00
4.4.-Radio de convergencia
Definición
Si nos limitamos al conjunto de los números reales, una serie de la forma , con , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
Ejemplos
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
.
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
Radio de convergencia infinito
Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho .
y esto vale para todo real x por eso el radio de convergencia será infinito.
Si nos limitamos al conjunto de los números reales, una serie de la forma , con , recibe el nombre de serie de potencias centrada en x0. La serie converge absolutamente para un conjunto de valores de x que verifica que | x − x0 | < r, donde r es un número real llamado radio de convergencia de la serie. Esta converge, pues, al menos, para los valores de x pertenecientes al intervalo (x0 − r, x0 + r), ya que la convergencia para los extremos de este ha de estudiarse aparte, por lo que el intervalo real de convergencia puede ser también semiabierto o cerrado. Si la serie converge solo para x0, r = 0. Si lo hace para cualquier valor de x, r =
Ejemplos
Mostraremos el radio de convergencia de algunos desarrollos en series de potencias con sus respectivos radios de convergencia sin justificar porqué el radio de convergencia es el dado.
Radio de convergencia finito
La función 1 / (1 − x) en su desarrollo con centro 0, o sea, en series de potencia x − x0 = x − 0 = x, tiene el siguiente aspecto:
.
(para el cálculo de la serie vea serie de Taylor). Su radio de convergencia es r = 1. Eso significa que para calcular si tomo cualquier valor cuya distancia al x0 = 0 es menor que r = 1, por ejemplo el x = 0.25, entonces al remplazarlo en la serie el resultado de calcular la serie será el mismo que remplazarlo en la función, de hecho
.
(la cuenta se puede hacer por serie de potencia). Y por otro lado
.
Pero si tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la serie, ésta diverja (por eso el nombre de radio de convergencia). Efectivamente:
Radio de convergencia infinito
Por ejempo, la función ex puede desarrollarse en series de potencia de x − 0 = x, de hecho .
y esto vale para todo real x por eso el radio de convergencia será infinito.
Publicado por Alejandro Reyes Rivero en 11:56
4.5 Series de taylor
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r).
sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1,3, 5, 7, 9, 11 y 13.
La función exponencial (en azul), y la suma de los primeros n+1 términos de su serie de Taylor en torno a cero (en rojo).
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Publicado por sinuhe en 10:09
miércoles, 25 de mayo de 2011
Representacion de funciones mediante la serie de taylor.
En matemáticas, una serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r).
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
Se puede utilizar para calcular valores aproximados de la función.
Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Definición:
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
que puede ser escrito de una manera más compacta como
donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor.
Si a = 0, a la serie se le llama serie de Maclaurin.
Esta representación tiene tres ventajas importantes:
La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
Se puede utilizar para calcular valores aproximados de la función.
Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Definición:
La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias:
que puede ser escrito de una manera más compacta como
donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
Suscribirse a:
Entradas (Atom)
